的確,K均值聚類和PCA似乎有非常不同的目標,乍一看似乎沒有關聯。但是,正如Ding & He 2004在論文通過主成分分析進行K-均值聚類所述,它們之間存在著深厚的聯繫。
直覺是PCA試圖代表所有 $ n $ span>數據向量都是少量特徵向量的線性組合,並且這樣做是為了最小化均方重構誤差。相反,K-means試圖通過少量簇質心來表示所有 $ n $ span>數據向量,即將它們表示為少量簇質心的線性組合向量,其中線性組合權重必須全部為零,但單個 $ 1 $ span>除外。這樣做也是為了最大程度地減少均方誤差。
因此,K均值可以看作是超稀疏PCA。
Ding &
不幸的是,Ding & He論文包含一些草率的表述(充其量),並且很容易被誤解。例如。他聲稱Ding &似乎證明了K-means聚類解決方案的聚類質心位於 $(K-1)$ span>維PCA子空間中:
定理3.3。群集質心子空間由第一個 $ K-1 $ span>主方向[...]跨越。
對於 $ K = 2 $ span>,這意味著PC1軸上的投影對於一個群集必定為負,而對於另一群集為正,即PC2軸將完美地分隔群集。
這是一個錯誤或一些草率的寫作;無論如何,從字面上看,該特定聲明都是錯誤的。
讓我們從2D中的 $ K = 2 $ span>玩具示例開始。我用相同的協方差矩陣但均值不同的兩個正態分佈生成了一些樣本。然後,我同時運行K-means和PCA。下圖顯示了上面數據的散點圖,並且根據下面的K-means解決方案對相同的數據進行了著色。我還將第一個主要方向顯示為黑線和K均值帶有黑色叉號的類質心。黑色虛線表示PC2軸。使用均一的隨機種子重複K均值 $ 100 $ span>次,以確保收斂到全局最優值。
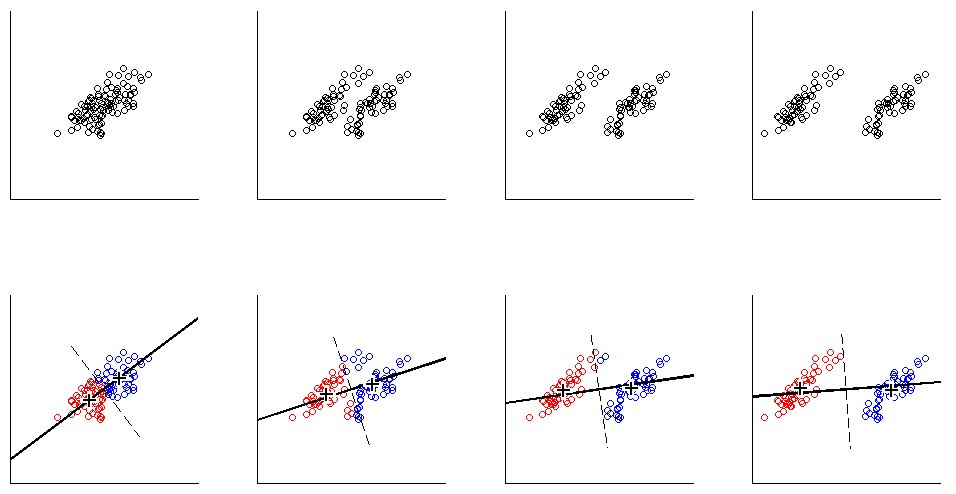
一個人可以清楚地看到,即使類質心傾向於非常接近第一個PC方向,它們也不會不恰好落在該方向上。而且,即使PC2軸在子圖1和圖4中完美地分隔了群集,在子圖2和3中,它的另一側也有一些點。
並且PCA相當不錯,但不完全準確。
那麼丁·艾里普姆·坎普(Ding &)他證明了什麼?為簡單起見,我僅考慮 $ K = 2 $ span>情況。假設分配給每個群集的點數為 $ n_1 $ span>和 $ n_2 $ span>,點 $ n = n_1 + n_2 $ span>。跟隨Ding & He,我們定義集群指標向量 $ \ mathbf q \ in \ mathbb R ^ n $ span>如下: $ i $ span> -th個點屬於聚類1和 $ q_i = \ sqrt {n_2 / nn_1} $ span> =“ math-container”> $ q_i =-\ sqrt {n_1 / nn_2} $ span>(如果它屬於群集2)。群集指示符向量的單位長度為 $ \ | \ mathbf q \ | = 1 $ span>並且“居中”,即其元素總和為零 $ \ sum q_i = 0 $ span>。
Ding &他證明了K均值損失函數 $ \ sum_k \ sum_i(\ mathbf x_i ^ {(k)}-\ boldsymbol \ mu_k)^ 2 $ span>(K-表示算法最小化),其中 $ x_i ^ {(k)} $ span>是 $ i $ span> -th群集 $ k $ span>中的元素可以等效地重寫為 $-\ mathbf q ^ \ top \ mathbf G \ mathbf q $ span>,其中 $ \ mathbf G $ span>是 $ n \ times n $ span>革蘭矩陣所有點之間的標量積: $ \ mathbf G = \ mathbf X_c \ mathbf X_c ^ \ top $ span>,其中 $ \ mathbf X $ span>是 $ n \ times2 $ span>數據矩陣和 $ \ mathbf X_c $ span >是岑 ter>
(注意:我使用的符號和術語與他們的論文略有不同,但我覺得更清楚)。
因此,K均值解決方案 $ \ mathbf q $ span>是最大化 $ \ mathbf q ^ \的居中單位向量。頂部\ mathbf G \ mathbf q $ span>。很容易看出,第一個主成分(當歸一化為具有平方的平方和時)是Gram矩陣的前導特徵向量,即它也是居中的單位向量 $ \ mathbf p $ span>最大化 $ \ mathbf p ^ \ top \ mathbf G \ mathbf p $ span>。唯一的區別是 $ \ mathbf q $ span>另外被約束為只有兩個不同的值,而 $ \ mathbf p $ 沒有此約束。
換句話說,K-means和PCA最大化相同的目標函數,唯一的區別是K-means具有附加的“類別”約束。
有理由認為,大多數情況下,K均值(約束)解決方案和PCA(無約束)解決方案非常接近彼此,因為我們在上面的模擬中看到過,但是不應期望它們是相同的。取 $ \ mathbf p $ span>並將其所有否定元素設置為等於 $-\ sqrt {n_1 / nn_2} $ span>及其對 $ \ sqrt {n_2 / nn_1} $ span>的所有肯定元素,通常不會準確地給出 Ding &他似乎很了解這一點,因為他們將其定理表示如下:
定理2.2 。對於其中 $ K = 2 $ span>的K均值聚類,聚類指示符矢量的連續解是[第一]主成分
請注意“連續解決方案”一詞。在證明了該定理之後,他們還評論說PCA可用於初始化K-means迭代,這很有意義,因為我們期望 $ \ mathbf q $ span>接近於 $ \ mathbf p $ span>。但是,仍然需要執行這些迭代,因為它們並不相同。
但是,丁&然後,他繼續為 $ K>2 $開發一種更通用的處理方法。 span>並最終將定理3.3公式化為
定理3.3。群集質心子空間由第一個 $ K-1 $ span>主方向跨越[...]。
我沒有去通過第3節的數學計算,但我相信該定理實際上也指K-means的“連續解”,即其陳述應為“ K-means連續解的聚類質心空間[。 。]“。
Ding &但是,他沒有取得這個重要的限定,並且在其摘要中寫道,
在這裡,我們證明主成分是對...的連續解。用於K均值聚類的離散聚類成員指標。等效地,我們表明,由簇質心跨越的子空間是由以 $ K-1 $ span>項截斷的數據協方差矩陣的譜擴展給出的。
第一句話是絕對正確的,但第二句話不是。 我不清楚這是(很)草率的文字還是真正的錯誤。我非常有禮貌地給兩位作者發了電子郵件,要求澄清。 (兩個月後更新:我再也沒有收到他們的來信。)
Matlab模擬代碼
figure('Position',[100100 1200 600])n = 50; Sigma = [2 1.8; 1.8 2];對於i = 1:4意味著= [0 0; i * 2 0]; ng(42)
X = [bsxfun(@plus,means(1,:),randn(n,2)* chol(Sigma)); ... bsxfun(@plus,means(2,:),randn(n,2)* chol(Sigma))]; X = bsxfun(@減,X,平均值(X)); [U,S,V] = svd(X,0); [ind,質心] = kmeans(X,2,'Replicates',100); subplot(2,4,i)散點圖(X(:,1),X(:,2),[],[0 0 0])subplot(2,4,i + 4)保持散點圖(X(ind == 1,1),X(ind == 1,2),[],[1 0 0])散點圖(X(ind == 2,1),X(ind == 2,2),[] ,[0 0 1])圖([-1 1] * 10 * V(1,1),[-1 1] * 10 * V(2,1),'k','LineWidth',2)圖(質心(1,1),質心(1,2),``w +'',``MarkerSize'',15,``線寬'',4)圖(質心(1,1),質心(1,2),``k +'' ,'MarkerSize',10,'LineWidth',2)plot(centroids(2,1),centroids(2,2),'w +','MarkerSize',15,'LineWidth',4)plot(centroids(2 ,1),重心(2,2),'k +','MarkerSize',10,'LineWidth',2)圖([-1-1] * 5 * V(1,2),[-1 1] * 5 * V(2,2),'k-')end for i = 1:8 subplot(2,4,i)axis([-8 8 -8 8])axis square set(gca,'xtick', [],'ytick',[])結束